Тренажер для изучения универсального исполнителя. Машина Тьюринга. Задачи и решения Понятие машины тьюринга
Маши́на Тью́ринга (МТ) - абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма .
Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча - Тьюринга , способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
Устройство машины Тьюринга
В состав машины Тьюринга входит бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство , способное находиться в одном из множества состояний . Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода , которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные , и переход в любое из них означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной , если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ - состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной .
Описание машины Тьюринга
Конкретная машина Тьюринга задаётся
перечислением элементов множества букв
алфавита A, множества состояний Q и
набором правил, по которым работает
машина. Они имеют вид: q i a j →q i1 a j1 d k
(если головка находится в состоянии q i ,
а в обозреваемой ячейке записана буква
a j , то головка переходит в состояние
q i1 , в ячейку вместо a j
записывается a j1 , головка делает
движение d k , которое имеет три
варианта: на ячейку влево (L), на ячейку
вправо (R), остаться на месте (N)). Для
каждой возможной конфигурации имеется ровно одно правило.
Правил нет только для заключительного
состояния, попав в которое машина
останавливается. Кроме того, необходимо
указать конечное и начальное состояния,
начальную конфигурацию на ленте и
расположение головки машины.
Пример машины Тьюринга
Приведём пример МТ для умножения чисел в унарной системе счисления . Машина работает по следующему набору правил:
|
Набор правил |
Набор правил |
|
q 0 ×→q 1 ×R |
|
|
q 6 ×→q 7 ×R |
|
|
q 2 ×→q 3 ×L |
|
|
q 3 1 → q 4 aR |
|
|
q 4 ×→q 4 ×R |
Умножим с помощью МТ 3 на 2 в единичной системе:
В протоколе указаны начальное и конечное состояния МТ, начальная конфигурация на ленте и расположение головки машины (подчёркнутый символ).
Полнота по Тьюрингу
Основная статья : Полнота по Тьюрингу
Можно сказать, что машина Тьюринга представляет собой простейшую вычислительную машину с линейной памятью, которая согласно формальным правилам преобразует входные данные с помощью последовательности элементарных действий .
Элементарность действий заключается в том, что действие меняет лишь небольшой кусочек данных в памяти (в случае машины Тьюринга - лишь одну ячейку), и число возможных действий конечно. Несмотря на простоту машины Тьюринга на ней можно вычислить всё, что можно вычислить на любой другой машине, осуществляющей вычисления с помощью последовательности элементарных действий. Это свойство называется полнотой .
Один из естественных способов доказательства того, что алгоритмы вычисления, которые можно реализовать на одной машине, можно реализовать и на другой, - это имитация первой машины на второй.
Имитация заключается в следующем. На вход второй машине подаётся описание программы (правил работы) первой машины D и входные данные X , которые должны были поступить на вход первой машины. Нужно описать такую программу (правила работы второй машины), чтобы в результате вычислений на выходе оказалось то же самое, что вернула бы первая машина, если бы получила на вход данные X .
Как было сказано, на машине Тьюринга можно имитировать (с помощью задания правил перехода) все другие исполнители, каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
На машине Тьюринга можно имитировать машину Поста , нормальные алгоритмы Маркова и любую программу для обычных компьютеров, преобразующую входные данные в выходные по какому-либо алгоритму. В свою очередь, на различных абстрактных исполнителях можно имитировать Машину Тьюринга. Исполнители, для которых это возможно, называются полными по Тьюрингу (Turing complete).
Есть программы для обычных компьютеров, имитирующие работу машины Тьюринга. Но следует отметить, что данная имитация неполная, так как в машине Тьюринга присутствует абстрактная бесконечная лента. Бесконечную ленту с данными невозможно в полной мере имитировать на компьютере с конечной памятью (суммарная память компьютера - оперативная память, жёсткие диски, различные внешние носители данных, регистры и кэш процессора и др. - может быть очень большой, но, тем не менее, всегда конечна).
Варианты машины Тьюринга
Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.
Машина Тьюринга, работающая на полубесконечной ленте
В качестве примера такого сведения рассмотрим следующую теорему: Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте.
Рассмотрим доказательство, приведённое Ю. Г. Карповым в книге «Теория автоматов». Доказательство этой теоремы конструктивное, то есть мы дадим алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Во-первых произвольно занумеруем ячейки рабочей ленты МТ, то есть определим новое расположение информации на ленте:
Затем перенумеруем ячейки, причём будем считать, что символ «*» не содержится в словаре МТ:

Наконец, изменим машину Тьюринга, удвоив число её состояний, и изменим сдвиг головки считывания-записи так, чтобы в одной группе состояний работа машины была бы эквивалентна её работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе МТ встретится символ ‘*’, значит головка считывания-записи достигла границы зоны:

Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации. Очевидно, что слева от ограничивающих маркеров «*» лента в эквивалентной машине Тьюринга не используется.
И, согласно тезису Чёрча - Тьюринга , способна имитировать всех исполнителей (с помощью задания правил перехода), каким-либо образом реализующих процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
То есть всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга .
Устройство
В состав машины Тьюринга входит неограниченная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки , и управляющее устройство (также называется головкой записи-чтения (ГЗЧ )), способное находиться в одном из множества состояний . Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода , которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные , и переход в любое из них означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной , если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ - состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной .
Описание машины Тьюринга
Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: q i a j →q i1 a j1 d k (если головка находится в состоянии q i , а в обозреваемой ячейке записана буква a j , то головка переходит в состояние q i1 , в ячейку вместо a j записывается a j1 , головка делает движение d k , которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации имеется ровно одно правило (для недетерминированной машины Тьюринга может быть большее количество правил). Правил нет только для заключительного состояния, попав в которое, машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.
Пример
Пример машины Тьюринга для умножения чисел в унарной системе счисления . Запись правила «q i a j →q i1 a j1 R/L/N» следует понимать так: q i - состояние при котором выполняется это правило, a j - данные в ячейке, в которой находится головка, q i1 - состояние в которое нужно перейти, a j1 - что нужно записать в ячейку, R/L/N - команда на перемещение.
Машина работает по следующему набору правил:
| q 0 | q 1 | q 2 | q 3 | q 4 | q 5 | q 6 | q 7 | q 8 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | q 0 1→q 0 1R | q 1 1→q 2 aR | q 2 1→q 2 1L | q 3 1 → q 4 aR | q 4 1→q 4 1R | q 7 1→q 2 aR | |||
| × | q 0 ×→q 1 ×R | q 2 ×→q 3 ×L | q 4 ×→q 4 ×R | q 6 ×→q 7 ×R | q 8 ×→q 9 ×N | ||||
| = | q 2 =→q 2 =L | q 4 =→q 4 =R | q 7 =→q 8 =L | ||||||
| a | q 2 a→q 2 aL | q 3 a→q 3 aL | q 4 a→q 4 aR | q 6 a→q 6 1R | q 7 a→q 7 aR | q 8 a→q 8 1L | |||
| * | q 0 *→q 0 *R | q 3 *→q 6 *R | q 4 *→q 5 1R | ||||||
| q 5 →q 2 *L |
Описание состояний:
| Начало | |
| q 0 | начальное состояние. Ищем «x» справа. При нахождении переходим в состояние q1 |
|---|---|
| q 1 | заменяем «1» на «а» и переходим в состояние q2 |
| Переносим все «1» из первого числа в результат | |
| q 2 | ищем «х» слева. При нахождении переходим в состояние q3 |
| q 3 | ищем «1» слева, заменяем её на «а» и переходим в состояние q4.
В случае если «1» закончились, находим «*» и переходим в состояние q6 |
| q 4 | переходим в конец (ищем «*» справа), заменяем «*» на «1» и переходим в состояние q5 |
| q 5 | добавляем «*» в конец и переходим в состояние q2 |
| Обрабатываем каждый разряд второго числа | |
| q 6 | ищем «х» справа и переходим в состояние q7. Пока ищем заменяем «а» на «1» |
| q 7 | ищем «1» или «=» справа
при нахождении «1» заменяем его на «а» и переходим в состояние q2 при нахождении «=» переходим в состояние q8 |
| Конец | |
| q 8 | ищем «х» слева. При нахождении переходим в состояние q9. Пока ищем заменяем «а» на «1» |
| q 9 | терминальное состояние (остановка алгоритма) |
Умножим с помощью МТ 3 на 2 в единичной системе. В протоколе указаны начальное и конечное состояния МТ, начальная конфигурация на ленте и расположение головки машины (подчёркнутый символ).
Начало. Находимся в состоянии q 0 , ввели в машину данные: *111x11=*, головка машины располагается на первом символе *.
1-й шаг. Смотрим по таблице правил что будет делать машина, находясь в состоянии q 0 и над символом «*». Это правило из 1-го столбца 5-й строки - q 0 *→q 0 *R. Это значит, что мы переходим в состояние q 0 (то есть не меняем его), символ станет «*» (то есть не изменится) и смещаемся по введённому нами тексту «*111x11=*» вправо на одну позицию (R), то есть на 1-й символ 1. В свою очередь, состояние q 0 1 (1-й столбец 1-я строка) обрабатывается правилом q 0 1→q 0 1R. То есть снова происходит просто переход вправо на 1 позицию. Так происходит, пока мы не станем на символ «х». И так далее: берём состояние (индекс при q), берём символ, на котором стоим (подчёркнутый символ), соединяем их и смотрим обработку полученной комбинации по таблице правил.
Простыми словами, алгоритм умножения следующий: помечаем 1-ю единицу 2-го множителя, заменяя её на букву «а», и переносим весь 1-й множитель за знак равенства. Перенос производится путём поочерёдной замены единиц 1-го множителя на «а» и дописывания такого же количества единиц в конце строки (слева от крайнего правого «*»). Затем меняем все «а» до знака умножения «х» обратно на единицы. И цикл повторяется. Действительно, ведь A умножить на В можно представить как А+А+А В раз. Помечаем теперь 2-ю единицу 2-го множителя буквой «а» и снова переносим единицы. Когда до знака «=» не окажется единиц - значит умножение завершено.
Полнота по Тьюрингу
Можно сказать, что машина Тьюринга представляет собой простейшую вычислительную машину с линейной памятью, которая согласно формальным правилам преобразует входные данные с помощью последовательности элементарных действий .
Элементарность действий заключается в том, что действие меняет лишь небольшой фрагмент данных в памяти (в случае машины Тьюринга - лишь одну ячейку), и число возможных действий не бесконечно. Несмотря на простоту машины Тьюринга, на ней можно вычислить всё, что можно вычислить на любой другой машине, осуществляющей вычисления с помощью последовательности элементарных действий. Это свойство называется полнотой .
Один из естественных способов доказательства того, что алгоритмы вычисления, которые можно реализовать на одной машине, можно реализовать и на другой, - это имитация первой машины на второй.
Имитация заключается в следующем. На вход второй машине подаётся описание программы (правил работы) первой машины D {\displaystyle D} и входные данные X {\displaystyle X} , которые должны были поступить на вход первой машины. Нужно описать такую программу (правила работы второй машины), чтобы в результате вычислений на выходе оказалось то же самое, что вернула бы первая машина, если бы получила на вход данные X {\displaystyle X} .
Как было сказано, на машине Тьюринга можно имитировать (с помощью задания правил перехода) все другие исполнители, каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
На машине Тьюринга можно имитировать машину Поста , нормальные алгоритмы Маркова и любую программу для обычных компьютеров, преобразующую входные данные в выходные по какому-либо алгоритму. В свою очередь, на различных абстрактных исполнителях можно имитировать Машину Тьюринга. Исполнители, для которых это возможно, называются полными по Тьюрингу (Turing complete).
Есть программы для обычных компьютеров, имитирующие работу машины Тьюринга. Но следует отметить, что данная имитация неполная, так как в машине Тьюринга присутствует абстрактная бесконечная лента. Бесконечную ленту с данными невозможно в полной мере имитировать на компьютере с конечной памятью: суммарная память компьютера - оперативная память, жёсткие диски, различные внешние носители данных, регистры и кэш процессора и др. - может быть очень большой, но, тем не менее, всегда конечна. Теоретический предел количества информации, которая может находиться внутри заданной поверхности, с точностью до множителя 1 / ln 2 {\displaystyle 1/\ln {2}} равен энтропии чёрной дыры с той же площадью поверхности.
Варианты машины Тьюринга
Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.
Машина Тьюринга, работающая на полубесконечной ленте
В качестве примера такого сведения рассмотрим следующую теорему: Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте (то есть на ленте, бесконечной в одну сторону).
Тема “Машина Тьюринга” в школьном курсе информатики
И.Н. Фалина,
Москва
Во многих учебниках по информатике при изучении понятия и свойств алгоритма присутствуют фразы такого содержания: “…существует много разных способов для записи одного и того же алгоритма, например, запись в виде текста, запись в виде блок-схемы, запись на каком-либо алгоритмическом языке, представление алгоритма в виде машины Тьюринга или машины Поста…”. К сожалению, такого типа фразы являются единственными, где упоминается машина Тьюринга. Без сомнения, объем часов, отводимых на изучение алгоритмов, не позволяет включать в эту тему еще и изучение способов записи алгоритма в виде машины Тьюринга. Но эта тема крайне интересна, важна и полезна для школьников, особенно увлекающихся информатикой.
Тема “Машина Тьюринга” может изучаться в 8–11-х классах в рамках темы “Информационные процессы. Обработка информации”, на факультативных занятиях, в системе дополнительного образования, например, в школах юных программистов. Изучение этой темы может сопровождаться компьютерной поддержкой, если у учителя есть программный тренажер-имитатор “Машина Тьюринга”. В классах с углубленным изучением программирования школьники могут самостоятельно написать программу “Машина Тьюринга”. В рамках этой статьи вашему вниманию предлагается практикум по решению задач на тему “Машина Тьюринга”. Теоретический материал по данной теме не раз печатался на страницах газеты “Информатика”, например, в № 3/2004 статья И.Н. Фалиной “Элементы теории алгоритмов”.
Краткий теоретический материал
Машина Тьюринга - это строгое математическое построение, математический аппарат (аналогичный, например, аппарату дифференциальных уравнений), созданный для решения определенных задач. Этот математический аппарат был назван “машиной” по той причине, что по описанию его составляющих частей и функционированию он похож на вычислительную машину. Принципиальное отличие машины Тьюринга от вычислительных машин состоит в том, что ее запоминающее устройство представляет собой бесконечную ленту: у реальных вычислительных машин запоминающее устройство может быть как угодно большим, но обязательно конечным. Машину Тьюринга нельзя реализовать именно из-за бесконечности ее ленты. В этом смысле она мощнее любой вычислительной машины.
В каждой машине Тьюринга есть две части:
1) неограниченная в обе стороны лента , разделенная на ячейки;
2) автомат (головка для считывания/записи, управляемая программой).
С каждой машиной Тьюринга связаны два конечных алфавита : алфавит входных символов A = {a 0 , a 1 , ..., a m }и алфавит состояний Q = {q 0 , q 1 , ..., q p }. (С разными машинами Тьюринга могут быть связаны разные алфавиты A и Q .) Состояние q 0 называется пассивным . Считается, что если машина попала в это состояние, то она закончила свою работу. Состояние q 1 называется начальным . Находясь в этом состоянии, машина начинает свою работу.
Входное слово размещается на ленте по одной букве в расположенных подряд ячейках. Слева и справа от входного слова находятся только пустые ячейки (в алфавит А всегда входит пустая буква а 0 - признак того, что ячейка пуста).
Автомат может двигаться вдоль ленты влево или вправо, читать содержимое ячеек и записывать в ячейки буквы. Ниже схематично нарисована машина Тьюринга, автомат которой обозревает первую ячейку с данными.
Автомат каждый раз “видит” только одну ячейку. В зависимости от того, какую букву ai он видит, а также в зависимости от своего состояния qj автомат может выполнять следующие действия:
- · записать новую букву в обозреваемую ячейку;
- · выполнить сдвиг по ленте на одну ячейку вправо/влево или остаться неподвижным;
- · перейти в новое состояние.
То есть у машины Тьюринга есть три вида операций. Каждый раз для очередной пары (q j , a i ) машина Тьюринга выполняет команду, состоящую из трех операций с определенными параметрами.
Программа для машины Тьюринга представляет собой таблицу, в каждой клетке которой записана команда.

Клетка (q j , a i ) определяется двумя параметрами - символом алфавита и состоянием машины. Команда представляет собой указание: куда передвинуть головку чтения/записи, какой символ записать в текущую ячейку, в какое состояние перейти машине. Для обозначения направления движения автомата используем одну из трех букв: “Л” (влево), “П” (вправо) или “Н” (неподвижен).
После выполнения автоматом очередной команды он переходит в состояние q m (которое может в частном случае совпадать с прежним состоянием q j ). Следующую команду нужно искать в m -й строке таблицы на пересечении со столбцом a l (букву a l автомат видит после сдвига).
Договоримся, что когда лента содержит входное слово, то автомат находится против какой-то ячейки в состоянии q 1. В процессе работы автомат будет перескакивать из одной клетки программы (таблицы) в другую, пока не дойдет до клетки, в которой записано, что автомат должен перейти в состояние q 0 . Эти клетки называются клетками останова . Дойдя до любой такой клетки, машина Тьюринга останавливается .
Несмотря на свое простое устройство, машина Тьюринга может выполнять все возможные преобразования слов, реализуя тем самым все возможные алгоритмы.
Пример. Требуется построить машину Тьюринга, которая прибавляет единицу к числу на ленте. Входное слово состоит из цифр целого десятичного числа, записанных в последовательные ячейки на ленте. В начальный момент машина находится против самой правой цифры числа.
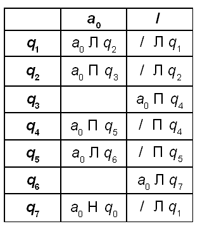
Решение. Машина должна прибавить единицу к последней цифре числа. Если последняя цифра равна 9, то ее заменить на 0 и прибавить единицу к предыдущей цифре. Программа для данной машины Тьюринга может выглядеть так:
В этой машине Тьюринга q 1 - состояние изменения цифры, q 0 - состояние останова. Если в состоянии q l автомат видит цифру 0..8, то он заменяет ее на 1..9 соответственно и переходит в состояние q 0 , т.е. машина останавливается. Если же он видит цифру 9, то заменяет ее на 0, сдвигается влево, оставаясь в состоянии q l . Так продолжается до тех пор, пока автомат не встретит цифру меньше 9. Если же все цифры были равны 9, то он заменит их нулями, запишет 0 на месте старшей цифры, сдвинется влево и в пустой клетке запишет 1. Затем перейдет в состояние q 0 , т.е. остановится.
Практические задания
1. На ленте машины Тьюринга содержится последовательность символов “+”. Напишите программу для машины Тьюринга, которая каждый второй символ “+” заменит на “–”. Замена начинается с правого конца последовательности. Автомат в состоянии q 1 обозревает один из символов указанной последовательности. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
2. Дано число n в восьмеричной системе счисления. Разработать машину Тьюринга, которая увеличивала бы заданное число n на 1. Автомат в состоянии q 1 обозревает некую цифру входного слова. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
3. Дана десятичная запись натурального числа n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1. Автомат в состоянии q 1 обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
4. Дано натуральное число n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1, при этом в выходном слове старшая цифра не должна быть 0. Например, если входным словом было “100”, то выходным словом должно быть “99”, а не “099”. Автомат в состоянии q 1 обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
5. Дан массив из открывающих и закрывающих скобок. Построить машину Тьюринга, которая удаляла бы пары взаимных скобок, т.е. расположенных подряд “()”.
Например, дано “) (() (()”, надо получить “) . . . ((”.
Автомат в состоянии q
6. Дана строка из букв “a ” и “b ”. Разработать машину Тьюринга, которая переместит все буквы “a ” в левую, а буквы “b ” - в правую части строки. Автомат в состоянии q 1 обозревает крайний левый символ строки. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
7. На ленте машины Тьюринга находится число, записанное в десятичной системе счисления. Умножить это число на 2. Автомат в состоянии q 1 обозревает крайнюю левую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
8. Даны два натуральных числа m и n , представленные в унарной системе счисления. Соответствующие наборы символов “|” разделены пустой клеткой. Автомат в состоянии q 1 обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит сумму чисел m и n . Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
9. Даны два натуральных числа m и n , представленных в унарной системе счисления. Соответствующие наборы символов “|” разделены пустой клеткой. Автомат в состоянии q 1 обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит разность чисел m и n . Известно, что m > n . Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
10. На ленте машины Тьюринга находится десятичное число. Определить, делится ли это число на 5 без остатка. Если делится, то записать справа от числа слово “да”, иначе - “нет”. Автомат обозревает некую цифру входного числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Решения заданий
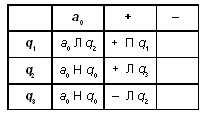
В состоянии q 1 машина ищет правый конец числа, в состоянии q 2 - пропускает знак “+”, при достижении конца последовательности - останавливается. В состоянии q 3 машина знак “+” заменяет на знак “–”, при достижении конца последовательности она останавливается.

Решение этой задачи аналогично рассмотренному выше примеру.
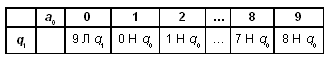
Состояние q 1 - уменьшаем младшую (очередную) цифру на 1. Если она не равна нулю, то после уменьшения сразу - останов, если же младшая цифра равна 0, то вместо нее пишем 9, смещаемся влево и вновь выполняем вычитание. В клетку [a 0 , q 1 ] машина Тьюринга никогда не попадет, поэтому ее можно не заполнять.
Задача 4 (усложнение задачи 3)
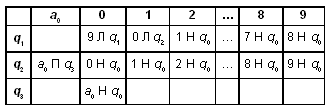
Состояние q 1 - уменьшаем младшую (очередную) цифру на 1. Если она больше 1, то после уменьшения - сразу останов, если же младшая цифра равна 0, то вместо нее пишем 9, смещаемся влево и вновь выполняем вычитание. Если уменьшаемая цифра равна 1, то вместо нее пишем 0 и переходим в состояние q 2 .
Состояние q 2 - после записи “0” в каком-либо разряде надо проанализировать, не является ли этот ноль старшей незначащей цифрой (т.е. не стоит ли слева от него в записи выходного слова a 0).
Состояние q 3 - если записанный “0” является старшей незначащей цифрой, то его надо удалить из записи выходного слова.
Те клетки, в которые машина Тьюринга никогда не попадает, оставляем пустыми.
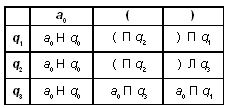
Состояние q 1: если встретили “(”, то сдвиг вправо и переход в состояние q 2 ; если встретили “a 0 ”, то останов.
Состояние q 2: анализ символа “(” на парность, в случае парности должны увидеть “)”. Если парная, то возврат влево и переход в состояние q 3 .
Состояние q 3: стираем сначала “(”, затем “)” и переходим в q 1 .
Решение этой задачи обычно вызывает у школьников затруднение. При разборе решения этой задачи можно пойти, например, следующим путем.
Рассмотрите со школьниками следующие варианты входных слов и попросите их сформулировать, что должна делать машина Тьюринга, каков внешний вид выходного слова, чем с точки зрения машины Тьюринга эти варианты различаются:
aaa ->
a -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.
bbb -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.
b -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.
ab -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.
Результат обсуждения. Машина Тьюринга должна “понимать”, по цепочке каких букв она идет, т.е. у нее должно быть как минимум два состояния. Пусть состояние q 1 - движение по цепочке из букв “a ”, а q 2 - состояние движения по цепочке из букв “b ”. Заметим, что цепочка может состоять и из одной буквы. Если мы дошли до конца строки в состоянии q 1 или q 2 , т.е. встретили a 0 , машина должна остановиться, мы обработали всю строку.
Рассмотрим следующие варианты входных слов:
bba -> abb
bbbaab -> aabbbb
aabbbaab -> aaaabbbb
Результат обсуждения. Первый вариант входного слова можно последовательно обработать следующим образом: bba -> bbb -> вернуться к левому концу цепочки из букв “b ” -> abb (заменить первую букву в этой цепочке на “a ”). Для выполнения этих действий нам потребуется ввести два новых состояния и, кроме того, уточнить состояние q 2 . Таким образом, для решения этой задачи нам нужно построить машину Тьюринга со следующими состояниями:
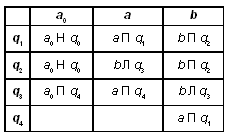
q 1 - идем вправо по цепочке букв “a ”. Если цепочка заканчивается a 0 , то переходим в q 0 ; если заканчивается буквой “b ”, то переходим в q 2 ;
q 2 - идем вправо по цепочке букв “b ”, если цепочка заканчивается a 0 , то переходим в q 0 ; если заканчивается “a ”, то заменяем букву “a ” на “b ”, переходим в состояние q 3 (цепочку вида заменили на цепочку вида );
q 3 - идем влево по цепочке букв “b ” до ее левого конца. Если встретили a 0 или “a ”, то переходим в q 4 ;
q 4 - заменяем “b ” на “a ” и переходим в q 1 (цепочку вида заменяем на цепочку вида .
Задача 7
состояние q 1 - поиск правой (младшей) цифры числа;
состояние q 2 -умножение очередной цифры числа на 2 без прибавления 1 переноса;
состояние q 3 - умножение очередной цифры числа на 2 с прибавлением 1 переноса.
Машина Тьюринга для этой программы выглядит тривиально просто - в ней всего одно состояние. Такая машина Тьюринга выполняет следующие действия: стирает самый правый штрих, ищет разделитель (пустую ячейку) и в эту пустую ячейку помещает штрих, тем самым сформирована непрерывная последовательность штрихов длины n + m .

Однако, как ни странно, решение этой задачи вызывает большие трудности. Очень часто ученики строят машину Тьюринга, которая выполняет циклические действия: последовательно пододвигают правые n штрихов к левым.
В этом случае их программа выглядит следующим образом:
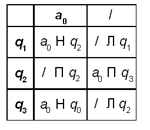
состояние q 1 -поиск разделителя;
состояние q 2 -передвинули штрих;
состояние q 3 -проверка на конец (все ли штрихи передвинули).
На примере этой задачи четко видно, как часто дети пытаются решить задачу уже знакомыми способами. Мне кажется, что, предлагая ученикам задачи на составление машин Тьюринга, мы развиваем способность к нахождению необычных решений, развиваем способность творчески думать!
Эта задача кажется школьникам достаточно легкой, но трудности возникают с остановом машины Тьюринга. Ниже приведен один из возможных вариантов машины Тьюринга для этой задачи.
Идея решения (условие останова). На ленте есть два исходных массива штрихов.
Штрихи начинаем стирать с левого конца массива m . И поочередно стираем самый левый штрих в массиве m и самый правый штрих в массиве n . Но прежде чем стереть правый штрих в массиве n , проверяем, единственный он (т.е. последний, который надо стереть) или нет.
Опишем сначала состояния машины Тьюринга, которые необходимы для решения нашей задачи, а затем составим программу-таблицу.
Состояние q 1 - поиск разделителя между массивами штрихов при движении справа налево;
состояние q 2 - поиск левого штриха в массиве m ;
состояние q 3 - удаление левого штриха в массиве m ;
состояние q 4 - поиск разделителя при движении слева направо;
состояние q 5 - поиск правого штриха в массиве n ;
состояние q 6 - проверка единственности этого штриха в массиве n , т.е. определяем, был ли он последним;
состояние q 7 - если он был последним, то останов, иначе переход на новый цикл выполнения алгоритма.
При решении этой задачи следует обратить внимание на правильное выписывание алфавита:
A = {a 0 , 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, Д, А, Н, Е, Т}.
Состояние q 1 -поиск правого конца числа;
состояние q 2 -анализ младшей цифры числа; если она равна “0” или “5”, т.е. число делится на 5, то переход в состояние q 3 , иначе переход в состояние q 5 ;
состояние q 3 -запись буквы “Д” справа от слова на ленте;
состояние q 4 -запись буквы “А” справа от слова и останов машины;
состояние q 5 -запись буквы “Н” справа от слова;
состояние q 6 -запись буквы “Е” справа от слова;
состояние q 7 -запись буквы “Т” справа от слова и останов машины.
Свойства машины Тьюринга как алгоритма
На примере машины Тьюринга хорошо прослеживаются свойства алгоритмов. Попросите учащихся показать, что машина Тьюринга обладает всеми свойствами алгоритма.
Дискретность. Машина Тьюринга может перейти к (к + 1)-му шагу только после выполнения к- го шага, т.к. именно к- й шаг определяет, каким будет (к + 1)-й шаг.
Понятность. На каждом шаге в ячейку пишется символ из алфавита, автомат делает одно движение (Л, П, Н), и машина Тьюринга переходит в одно из описанных состояний.
Детерминированность. В каждой клетке таблицы машины Тьюринга записан лишь один вариант действия. На каждом шаге результат определен однозначно, следовательно, последовательность шагов решения задачи определена однозначно, т.е. если машине Тьюринга на вход подают одно и то же входное слово, то выходное слово каждый раз будет одним и тем же.
Результативность. Содержательно результаты каждого шага и всей последовательности шагов определены однозначно, следовательно, правильно написанная машина Тьюринга за конечное число шагов перейдет в состояние q 0, т.е. за конечное число шагов будет получен ответ на вопрос задачи.
Массовость. Каждая машина Тьюринга определена над всеми допустимыми словами из алфавита, в этом и состоит свойство массовости. Каждая машина Тьюринга предназначена для решения одного класса задач, т.е. для каждой задачи пишется своя (новая) машина Тьюринга.
ОТ РЕДАКЦИИ
Все приведенные в статье задачи можно решить просто в тетради, начертив информационную ленту и программу-таблицу. Но можно сделать этот процесс более увлекательным и наглядным: воспользоваться машинной реализацией - интерпретатором машины Поста и машины Тьюринга “Algo2000”, созданным Радиком Зартдиновым. Программа обладает интуитивно понятным интерфейсом, и требования у нее самые умеренные: компьютер IBM PC AT 486 и выше, наличие операционной системы Windows"95/98/NT.
Посмотрим в общих чертах, как работает “Algo2000”.
В меню программы выберем пункт Интерпретатор и укажем, с какой машиной мы хотим работать (в нашем случае это “машина Тьюринга”).
Перед нами появится поле машины Тьюринга.
Теперь необходимо задать внешний алфавит, т.е. в строке Внешний алфавит указать, какие символы в него входят (если строка Внешний алфавит не видна, нужно выбрать пункт меню Вид | Внешний алфавит ). Каждый символ можно указать только один раз. После окончания ввода внешнего алфавита формируется первый столбец таблицы: он заполняется символами внешнего алфавита в том же порядке. При редактировании внешнего алфавита автоматически изменяется таблица: вставляются, удаляются или меняются местами строки.
Не забудем, что нужно как-то расставить символы внешнего алфавита по секциям ленты (можно все секции оставить пустыми) и поставить каретку против одной из секций, т.е. надо задать программу и некоторое состояние машины.
Теперь можно приступить непосредственно к записи алгоритма решения задачи. Он задается в виде таблицы: в каждый столбец верхней строчки заносятся символы внутреннего алфавита, в каждую строчку первого столбца - символы внешнего алфавита. В ячейках на пересечении других столбцов и строчек помещаются команды. Если на пересечении какой-либо строки и какого-либо столбца мы получим пустую клетку, то это означает, что в данном внутреннем состоянии данный символ встретиться не может.
Например, мы составляем алгоритм нахождения разности двух целых положительных чисел (в десятичной системе счисления), если известно, что первое число больше второго, а между ними стоит знак минус.
Поле программы будет выглядеть так:

Формат команды в каждой ячейке - aKq.
Здесь:
a - новое содержание текущей ячейки (новый символ
внешнего алфавита, который заносится в текущую
ячейку), K - команда лентопротяжного механизма
машины Тьюринга (влево, вправо, стоп), q - новое
внутреннее состояние машины Тьюринга.
Кнопка запустит программу. Если выполнение не было приостановлено, то оно всегда начинается с нулевого внутреннего состояния Q0.
Программу можно выполнить по шагам. Для этого нажмите на кнопку на панели инструментов (если кнопки не видны, нужно выбрать пункт меню Вид | Панель инструментов ) или выберите в главном меню Пуск | Пошагово . Если необходимо полностью прервать выполнение программы, то это можно сделать с помощью кнопки на панели инструментов или с помощью главного меню (Пуск | Прервать ). Пункт меню Скорость позволяет регулировать скорость выполнения программы.
Выполнение программы будет идти до тех пор, пока не встретится команда “Стоп” или не возникнет какая-нибудь ошибка.
При возникновении вопросов в ходе работы с программой-интерпретатором обращайтесь к справочному файлу Algo2000.hlp . Его, так же, как и саму программу “Algo2000”, можно найти на сайте газеты “Информатика” http://inf.1september.ru в разделе “Download”.
Транскрипт
1 Московский государственный университет им. М.В. Ломоносова Факультет вычислительной математики и кибернетики В.Н. Пильщиков, В.Г. Абрамов, А.А. Вылиток, И.В. Горячая Машина Тьюринга и алгоритмы Маркова. Решение задач (Учебно-методическое пособие) Москва, 2006

2 УДК ББК П32 Пильщиков В.Н., Абрамов В.Г., Вылиток А.А., Горячая И.В. Машина Тьюринга и алгоритмы Маркова. Решение задач. (Учебно-методическое пособие) - М.: МГУ, с. Издательский отдел факультета ВМК МГУ (лицензия ЛР от) Пособие посвящено решению задач по теме «Введение в теорию алгоритмов», изучаемой на первом курсе факультета ВМК МГУ в рамках дисциплины «Алгоритмы и алгоритмические языки». Это задачи на составление алгоритмов в виде машины Тьюринга и нормальных алгоритмов Маркова, а также задачи теоретического характера. В пособии приводятся необходимые сведения по теории алгоритмов, подробно объясняются типичные приёмы решения задач и предлагается большой набор задач для самостоятельного решения. Пособие рассчитано на студентов первого курса факультета ВМК МГУ и преподавателей, ведущих семинарские занятия по программированию. Рецензенты: доцент Баула В.Г. доцент Корухова Л.С. Печатается по решению Редакционно-издательского совета факультета вычислительной математики и кибернетики МГУ им. М.В. Ломоносова. ISBN??? Издательский отдел факультета вычислительной математики и кибернетики МГУ им. М.В. Ломоносова,

3
1. Машина Тьюринга В разделе рассматриваются задачи на составление алгоритмов для машины Тьюринга. Приводится краткое описание этой машины, на примерах объясняются основные приёмы составления таких алгоритмов и предлагаются задачи для самостоятельного решения. 1.1 Краткое описание машины Тьюринга Структура машины Тьюринга Машина Тьюринга (МТ) состоит из двух частей ленты и автомата (см. слева): лента: a b b Λ Λ a b b Λ Λ автомат: q q Лента используется для хранения информации. Она бесконечна в обе стороны и разбита на клетки, которые никак не нумеруются и не именуются. В каждой клетке может быть записан один символ или ничего не записано. Содержимое клетки может меняться в неё можно записать другой символ или стереть находящийся там символ. Договоримся пустое содержимое клетки называть символом «пусто» и обозначать знаком Λ («лямбда»). В связи с этим изображение ленты, показанное на рисунке справа, такое же, как и на рисунке слева. Данное соглашение удобно тем, что операцию стирания символа в некоторой клетке можно рассматривать как запись в эту клетку символа Λ, поэтому вместо длинной фразы «записать символ в клетку или стереть находящийся там символ» можно говорить просто «записать символ в клетку». Автомат это активная часть МТ. В каждый момент он размещается под одной из клеток ленты и видит её содержимое; это видимая клетка, а находящийся в ней символ видимый символ; содержимое соседних и других клеток автомат не видит. Кроме того, в каждый момент автомат находится в одном из состояний, которые будем обозначать буквой q с номерами: q1, q2 и т.п. Находясь в некотором состоянии, автомат выполняет какую-то определённую операцию (например, перемещается направо по ленте, заменяя все символы b на a), находясь в другом состоянии другую операцию. Пару из видимого символа (S) и текущего состояния автомата (q) будем называть конфигурацией и обозначать

4 Такт работы машины Тьюринга МТ работает тактами, которые выполняются один за другим. На каждом такте автомат МТ выполняет три следующих действия, причем обязательно в указанном порядке: 1) записывает некоторый символ S в видимую клетку (в частности, может быть записан тот же символ, что и был в ней, тогда содержимое этой клетки не меняется); 2) сдвигается на одну клетку влево (обозначение L, от left), либо на одну клетку вправо (обозначение R, от right), либо остается неподвижным (обозначение N). 3) переходит в некоторое состояние q (в частности, может остаться в прежнем состоянии). Формально действия одного такта будем записывать в виде тройки: S, , q где конструкция с квадратными скобками означает возможность записи в этом месте любой из букв L, R или N. Например, такт *,L,q8 означает запись символа * в видимую клетку, сдвиг на одну клетку влево и переход в состояние q8. Программа для машины Тьюринга Сама по себе МТ ничего не делает. Для того чтобы заставить её работать, надо написать для неё программу. Эта программа записывается в виде следующей таблицы: q 1 q j q m S 1 S 2 S i S n Λ S, , q Слева перечисляются все состояния, в которых может находиться автомат, сверху все символы (в том числе и Λ), которые автомат может видеть на ленте. (Какие именно символы и состояния указывать в таблице определяет автор программы.) На пересечениях же (в ячейках таблицы) указываются те такты, которые должен выполнить автомат, когда он находится в соответствующем состоянии и видит на ленте соответствующий символ. В целом таблица определяет действия МТ при всех возможных конфигурациях и тем самым полностью задаёт поведение МТ. Описать алгоритм в виде МТ значит предъявить такую таблицу. (Замечание. Часто МТ определяют как состоящую из ленты, автомата и программы, поэтому при разных программах получаются разные МТ. Мы же будет считать, в духе современных компьютеров, что МТ одна, но она может выполнять разные программы.) 4

5
Правила выполнения программы До выполнения программы нужно проделать следующие предварительные действия. Во-первых, надо записать на ленту входное слово, к которому будет применена программа. Входное слово это конечная последовательность символов, записанных в соседних клетках ленты; внутри входного слова пустых клеток быть не должно, а слева и справа от него должны быть только пустые клетки. Пустое входное слово означает, что все клетки ленты пусты. Во-вторых, надо установить автомат в состояние q 1 (указанное в таблице первым) и разместить его под первым символом входного слова: a b b q 1 Если входное слово пустое, то автомат может смотреть в любую клетку, т.к. все они пусты. После этих предварительных действий начинается выполнение программы. В таблице отыскивается ячейка на пересечении первой строки (т.к. автомат находится в состоянии q 1) и того столбца, который соответствует первому символу входного слова (это необязательно левый столбец таблицы), и выполняется такт, указанный в этой ячейке. В результате автомат окажется в новой конфигурации. Теперь такие же действия повторяются, но уже для новой конфигурации: в таблице отыскивается ячейка, соответствующая состоянию и символу этой конфигурации, и выполняется такт из этой ячейки. И так далее. Когда завершается выполнение программы? Введём понятие такта останова. Это такт, который ничего не меняет: автомат записывает в видимую клетку тот же символ, что и был в ней раньше, не сдвигается и остается в прежнем состоянии, т.е. это такт S,N,q для конфигурации

6
2) Второй исход «плохой»: это когда МТ зацикливается, никогда не попадая на такт останова (например, автомат на каждом шаге сдвигается вправо и потому не может остановиться, т.к. лента бесконечна). В этом случае говорят, что МТ неприменима к заданному входному слову. Ни о каком результате при таком исходе не может идти и речи. Отметим, что один и тот же алгоритм (программа МТ) может быть применимым к одним входным словам (т.е. останавливаться) и неприменимым к другим (т.е. зацикливаться). Таким образом, применимость/неприменимость зависит не только от самого алгоритма, но и от входного слова. На каких входных словах алгоритм должен останавливаться? На, так сказать, хороших словах, т.е. на тех, которые относятся к допустимым исходным данным решаемой задачи, для которых задача осмысленна. Но на ленте могут быть записаны любые входные слова, в том числе и те, для которых задача не имеет смысла; на таких словах поведение алгоритма не фиксируется, он может остановиться (при любом результате), а может и зациклиться. Соглашения для сокращения записи Договоримся о некоторых соглашениях, сокращающих запись программы для МТ. 1) Если в такте не меняется видимый символ, или автомат не сдвигается, или не меняется состояние автомата, то в соответствующей позиции такта мы не будем ничего писать. Например, при конфигурации

7 1.2 Примеры на составление программ для МТ Рассмотрим примеры на составление программ для МТ, чтобы продемонстрировать некоторые типичные приёмы программирования на МТ. Для сокращения формулировки задач введём следующие два соглашения: буквой Р будем обозначать входное слово; буквой А будем обозначать алфавит входного слова, т.е. набор тех символов, из которых и только которых может состоять Р (отметим, однако, что в промежуточных и выходном словах могут появляться и другие символы). Пример 1 (перемещение автомата, замена символов) А={0,1,2,3,4,5,6,7,8,9}. Пусть Р непустое слово; значит, Р это последовательность из десятичных цифр, т.е. запись неотрицательного целого числа в десятичной системе. Требуется получить на ленте запись числа, которое на 1 больше числа Р. Решение. Для решения этой задачи предлагается выполнить следующие действия: 1. Перегнать автомат под последнюю цифру числа. 2. Если это цифра от 0 до 8, то заменить её цифрой на 1 больше и остановиться; например: Если же это цифра 9, тогда заменить её на 0 и сдвинуть автомат к предыдущей цифре, после чего таким же способом увеличить на 1 эту предпоследнюю цифру; например: Особый случай: в Р только девятки (например, 99). Тогда автомат будет сдвигаться влево, заменяя девятки на нули, и в конце концов окажется под пустой клеткой. В эту пустую клетку надо записать 1 и остановиться (ответом будет 100): В виде программы для МТ эти действия описываются следующим образом: Λ q1 0,R,q1 1,R,q1 2,R,q1 3,R,q1 4,R,q1 5,R,q1 6,R,q1 7,R,q1 8,R,q1 9,R,q1 Λ,L,q2 q2 1,N,! 2, N,! 3, N,! 4, N,! 5, N,! 6, N,! 7, N,! 8, N,! 9, N,! 0,L,q2 1,N,! Пояснения. q1 это состояние, в котором автомат «бежит» под последнюю цифру числа. Для этого он всё время движется вправо, не меняя видимые цифры и оставаясь в том же состоянии. Но здесь есть одна особенность: когда автомат находится под 7

8 последней цифрой, то он ещё не знает об этом (ведь он не видит, что записано в соседних клетках) и определит это лишь тогда, когда попадёт на пустую клетку. Поэтому, дойдя до первой пустой клетки, автомат возвращается назад под последнюю цифру и переходит в состояние q2 (вправо двигаться уже не надо). q2 это состояние, в котором автомат прибавляет 1 к той цифре, которую видит в данный момент. Сначала это последняя цифра числа; если она в диапазоне от 0 до 8, то автомат заменяет её цифрой, которая на 1 больше, и останавливается. Но если это цифра 9, то автомат заменяет её на 0 и сдвигается влево, оставаясь в состоянии q2. Тем самым, он будет теперь прибавлять 1 к предыдущей цифре. Если и эта цифра равна 9, то автомат заменяет её на 0 и сдвигается влево, оставаясь попрежнему в состоянии q2, т.к. должен выполнить то же самое действие увеличить на 1 видимую цифру. Если же автомат сдвинулся влево, а в видимой клетке нет цифры (а есть «пусто»), то он записывает сюда 1 и останавливается. Отметим, что для пустого входного слова наша задача не определена, поэтому на этом слове МТ может вести себя как угодно. В нашей программе, например, при пустом входном слове МТ останавливается и выдает ответ 1. Выше мы привели запись программы в полном, несокращённом виде. Теперь же приведём запись программы в сокращённом, более наглядном виде, при этом справа дадим краткое пояснение действий, которые реализуются в соответствующих состояниях автомата: Λ q1,r,r,r,r,r,r,r,r,r,r,l,q2 под последнюю цифру q2 1,! 2,! 3,! 4,! 5,! 6,! 7,! 8,! 9,! 0,L, 1,! видимая цифра + 1 Именно так мы и будем в дальнейшем записывать программы. Пример 2 (анализ символов) А={a,b,c}. Перенести первый символ непустого слова Р в его конец. Например: a b c b b c b a Решение. Для решения этой задачи предлагается выполнить следующие действия: 1. Запомнить первый символ слова P, а затем стереть этот символ. 2. Перегнать автомат вправо под первую пустую клетку за P и записать в неё запомненный символ. Как «бегать» вправо, мы уже знаем из предыдущего примера. А вот как запомнить первый символ? Ведь в МТ нет другого запоминающего устройства, кроме ленты, а запоминать символ в какой-то клетке на ленте бессмысленно: как только автомат сдвинется влево или вправо от этой клетки, он тут же забудет данный символ. Что делать? Выход здесь таков надо использовать разные состояния автомата. Если первый символ это a, то надо перейти в состояние q2, в котором автомат 8

9 бежит вправо и записывает в конце a. Если же первым был символ b, тогда надо перейти в состояние q3, где делается всё то же самое, только в конце записывается символ b. Если же первым был символ c, тогда переходим в состояние q4, в котором автомат дописывает за входным словом символ c. Следовательно, то, каким был первый символ, мы фиксируем переводом автомата в разные состояния. Это типичный приём при программировании на МТ. С учётом сказанного программа будет такой: a b c Λ q1 Λ,R,q2 Λ,R,q3 Λ,R,q4,R, анализ 1-го символа, удаление его, разветвление q2,r,r,r, a,! запись a справа q3,r,r,r, b,! запись b справа q4,r,r,r, c,! запись c справа Рассмотрим поведение этой программы на входных словах, содержащих не более одного символа. При пустом слове, которое является «плохим» для задачи, программа зациклится автомат, находясь в состоянии q1 и попадая всё время на пустые клетки, будет бесконечно перемещаться вправо. (Конечно, в этом случае программу можно было бы остановить, но мы специально сделали зацикливание, чтобы продемонстрировать такую возможность.) Если же во входном слове ровно один символ, тогда автомат сотрёт этот символ, сдвинется на одну клетку вправо и запишет в неё данный символ: c c q1 q4! Таким образом, слово из одного символа попросту сдвинется на клетку вправо. Это допустимо. Ведь клетки ленты не нумерованы, поэтому местоположение слова на ленте никак не фиксируется и перемещение слова влево или вправо заметить нельзя. В связи с этим не требуется, чтобы выходное слово обязательно находилось в том же месте, где было входное слово, результат может оказаться и левее, и правее этого места. Пример 3 (сравнение символов, стирание слова) А={a,b,c}. Если первый и последний символы (непустого) слова Р одинаковы, тогда это слово не менять, а иначе заменить его на пустое слово. Решение. Для решения этой задачи предлагается выполнить следующие действия: 1. Запомнить первый символ входного слова, не стирая его. 2. Переместить автомат под последний символ и сравнить его с запомненным. Если они равны, то больше ничего не делать. 3. В противном случае уничтожить всё входное слово. Как запоминать символ и как перегонять автомат под последний символ слова, мы уже знаем из предыдущих примеров. Стирание же входного слова реализуется 9

10 заменой всех его символов на символ Λ. При этом, раз уж автомат оказался в конце слова, будем перемещать автомат справа налево до первой пустой клетки. Эти действия описываются следующей программой для МТ (напомним, что крестик в ячейке таблицы означает невозможность появления соответствующей конфигурации при выполнении программы): a b c Λ q1,q2,q4,q6,! анализ 1-го символа, разветвление q2,r,r,r, L,q3 идти к последнему символу при 1-м символе a q3,!, q8, q8 сравнить посл. символ с a, не равны на q8 (стереть P) q4,r,r,r, L,q5 аналогично при 1-м символе b q5, q8,!, q8 q6,r,r,r, L,q7 аналогично при 1-м символе c q7, q8, q8,! q8 Λ,L, Λ,L, Λ,L,! стереть всё слово, двигаясь справа налево Пример 4 (удаление символа из слова) А={a,b}. Удалить из слова Р его второй символ, если такой есть. Решение. Казалось бы, эту задачу решить просто: надо сдвинуть автомат под клетку со вторым символом и затем очистить эту клетку: a b b a a b b a a b a Однако напомним, что внутри выходного слова не должно быть пустых клеток. Поэтому после удаления второго символа надо «сжать» слово, перенеся первый символ на одну клетку вправо. Для этого автомат должен вернуться к первому символу, запомнить его и стереть, а затем, снова сдвинувшись вправо, записать его в клетку, где был второй символ. Однако начальный «поход» вправо ко второму символу, чтобы его стереть, и последующий возврат к первому символу являются лишними действиями: какая разница переносить первый символ в пустую клетку или в клетку с каким-то символом? Поэтому сразу запоминаем первый символ, стираем его и записываем вместо второго символа: a b b a b b a a b a В виде программы для МТ всё это записывается так: a b Λ q1 Λ,R,q2 Λ,R,q3,! анализ и удаление 1-го символа, разветвление q2,! a,! a,! замена 2-го символа на a q3 b,!,! b,! замена 2-го символа на b Пример 5 (сжатие слова) А={a,b,c}. Удалить из слова Р первое вхождение символа a, если такое есть. Решение. В предыдущем примере мы переносили на позицию вправо только один сим- 10

11
вол. В данном же примере мы будем в цикле переносить вправо все начальные символы b и c входного слова до первого символа a или до пустой клетки: b c b c b a a b b a a b c a a b c b a Центральный момент здесь как перенести символ x из левой клетки в очередную клетку, где находится некоторый символ y, чтобы затем этот символ y можно было перенести в правую клетку? Если через q x обозначить состояние, в котором в видимую клетку надо записать символ x, находившийся ранее в клетке слева, тогда это действие можно изобразить так: x y y z x z q x Для этого предлагается выполнить такт x,r,q y, в котором объединены следующие три действия: во-первых, в видимую клетку записывается символ x, взятый из клетки слева; во-вторых, автомат сдвигается вправо под клетку, в которую затем надо будет записать только что заменённый символ y; в-третьих, автомат переходит в состояние q y, в котором он и будет выполнять эту запись. Повторение таких тактов в цикле и приведёт к сдвигу вправо на одну позицию начальных символов входного слова. Этот цикл должен закончиться, когда в очередной клетке окажется символ a или Λ (y=a или y=λ), а в начале цикла можно считать, что на место первого символа слева переносится символ «пусто» (x=λ). В итоге получается следующая программа для МТ: a b c Λ q1 Λ,R,! Λ,R,q2 Λ,R,q3,! q Λ : стереть 1-й символ и перенести его вправо q2 b,!,r, b,r,q3 b,! q b: запись b, перенос ранее видимого символа вправо q3 c,! c,r,q2,r, c,! q c: запись c, перенос ранее видимого символа вправо В этой программе следует обратить внимание на такт Λ,R,!, который выполняется в конфигурации

12 первый символ (на старом месте его можно пока не удалять), а затем, вернувшись на старое место, записать символ a: b c a b c a b b c a b a c a Перенос символа на одну позицию влево аналогичен переносу символа вправо, о чём говорилось в двух предыдущих примерах, поэтому приведем программу для МТ без дополнительных комментариев. Отметим лишь, что в состояниях q2, q3 и q4 автомат может видеть только пустую клетку, а в состоянии q5 он обязательно видит первый символ входного слова, но не пустую клетку. a b c Λ q1,l,q2,l,q3,l,q4,! анализ 1-го символа для переноса его влево q2 a,r,q5 приписать a слева q3 b,r,q5 приписать b слева q4 c,r,q5 приписать c слева q5,! a,! a,! заменить бывший 1-й символ на a Пример 7 (раздвижка слова) А={a,b,c}. Вставить в слово P символ a за первым вхождением символа c, если такое есть. Решение. Просматриваем входное слово слева направо до пустой клетки или до первого символа c. В первом случае c не входит в P, поэтому ничего не делаем. Во втором случае надо освободить место для вставляемого символа a, для чего сдвигаем начало слова P (от первого символа до найденного символа c) на одну позицию влево. При этом осуществляем такой сдвиг справа налево от символа c к началу слова, раз уж автомат находится под этим символом. Кроме того, чтобы затем не возвращаться к освободившейся позиции, начинаем этот сдвиг с записи a вместо найденного символа c. Поскольку этот циклический сдвиг влево реализуется аналогично циклическому сдвигу вправо из примера 5, то не будем пояснять его, а сразу приведём программу для МТ: a b c Λ q1,r,r, a,l,q4,l,! вправо до с, вставка a вместо c, перенос c влево q2,l, a,l,q3 a,l,q4 a,! перенос a справа q3 b,l,q2,l, b,l,q4 b,! перенос b справа q4 c,l,q2 c,l,q3,l, c,! перенос c справа Пример 8 (формирование слова на новом месте) А={a,b,c}. Удалить из P все вхождения символа a. Решение. Предыдущие примеры показывают, что в МТ достаточно сложно реализуются вставки символов в слова и удаления символов из слов. Поэтому иногда проще не раздвигать или сжимать входное слово, а формировать выходное сло- 12

13 во в другом, свободном месте ленты. Именно так мы и поступим при решении данной задачи. Конкретно предлагается выполнить следующие действия: 1. Выходное слово будем строить справа от входного. Чтобы разграничить эти слова, отделим их некоторым вспомогательным символом, например знаком =, отличным от всех символов алфавита A (см. шаг 1). (Напомним, что на ленте могут быть записаны не только символы из алфавита входного слова.) 2. После этого возвращаемся к началу входного слова (см. шаг 2). a b c a b c = a b c = Теперь наша задача перенести в цикле все символы входного слова, кроме a, вправо за знак = в формируемое выходное слово. Для этого анализируем первый символ входного слова. Если это a, тогда стираем его и переходим к следующему символу (см. шаг 3). Если же первый символ это b или c, тогда стираем его и «бежим» вправо до первой пустой клетки (см. шаг 4), куда и записываем этот символ (см. шаг 5). b c = c = c = b Снова возвращаемся налево к тому символу, который стал первым во входном слове, и повторяем те же самые действия, но уже по отношению к этому символу (см. шаги 6-9). c = b = b = b c Этот цикл завершается, когда при возврате налево мы увидим в качестве первого символа знак =. Это признак того, что мы полностью просмотрели входное слово и перенесли все его символы, отличные от a, в формируемое справа выходное слово. Надо этот знак стереть, сдвинуться вправо под выходное слово и остановиться (см. шаг 10). = b c b c 9 10 С учётом всего сказанного и строим программу для МТ. При этом отметим, что помимо символов a, b и c в процессе решения задачи на ленте появляется знак =, поэтому в таблице должен быть предусмотрен столбец и для этого знака. a b c = Λ q1,r,r,r, =,q2 записать справа знак = q2,l,l,l,l,r,q3 влево к 1-му символу слова q3 Λ,R, Λ,R,q4 Λ,R,q5 Λ,R,! анализ и удаление его, разветвление q4,r,r,r,r, b,q2 запись b справа, возврат налево (в цикл) q5,r,r,r,r, c,q2 запись c справа, возврат налево (в цикл) 13

14 Пример 9 (фиксирование места на ленте) А={a,b}. Удвоить слово P, поставив между ним и его копией знак =. Например: a a b a a b = a a b Решение. Эта задача решается аналогично предыдущей: в конец входного слова записываем знак =, затем возвращаемся к началу слова и в цикле все его символы (в том числе и a) копируем в пустые клетки справа: a a b a a b = a a b = a a b = a 1 2 Однако есть и отличие: копируемые символы входного слова не удаляются, и это приводит к следующей проблеме. Записав справа копию очередного символа, мы затем должны вернуться к входному слову в позицию этого символа и потом сдвинуться вправо к следующему символу, чтобы скопировать уже его. Но как узнать, в какую позицию входного слова надо вернуться? Например, откуда мы знаем в нашем примере, что после копирования первого символа a мы должны вернуться именно к первому символу входного слова, а не ко второму или третьему? В предыдущей задаче мы всегда возвращались к первому из оставшихся символов входного слова, а теперь мы сохраняем все символы, поэтому непонятно, какие символы мы уже скопировали, а какие ещё нет. Отметим также, что в МТ ячейки ленты никак не нумеруются, нет в МТ и счетчиков, которые позволили бы определить, сколько символов мы уже скопировали. В общем виде проблема, с которой мы столкнулись, следующая: как зафиксировать на ленте некоторую позицию, в которой мы уже были и к которой позже должны вернуться? Обычно эта проблема решается так. Когда мы оказываемся в этой позиции в первый раз, то заменяем находящийся в ней символ на его двойник на новый вспомогательный символ, причем разные символы заменяем на разные двойники, например a на A и b на B. После этого мы выполняем какие-то действия в других местах ленты. Чтобы затем вернуться к нашей позиции, надо просто отыскать на ленте ту клетку, где находится символ A или B. Затем в данной клетке можно восстановить прежний символ, если нам больше не надо фиксировать эту позицию (именно для восстановления прежнего символа и надо было заменять разные символы на разные двойники). Воспользуемся этим приёмом в нашей задаче, выполняя следующие действия: 1. Как уже сказано, вначале записываем знак = за входным словом (см. шаг 1 выше). 2. Затем возвращаемся под первый символ входного слова (см. шаг 2 выше). 3. Далее заменяем видимый символ a на двойник A (см. шаг 3 ниже), «бежим» вправо до первой свободной клетки и записываем в неё символ a (см. шаг 4). После этого возвращаемся влево к клетке с двойником A (см. шаг 5), восстанавливаем прежний символ a и сдвигаемся вправо к следующему символу (см. шаг 6). 14

15 a a b = A a b = A a b = a A a b = a a a b = a a A b = a a A b = a a a a B = a a b a a b = a a b Теперь аналогичным образом копируем второй символ (заменяем его на A, в конец дописываем a и т.д.) и все последующие символы входного слова. 4. Когда мы скопируем последний символ входного слова и вернёмся к его двойнику (после шага 12), то затем после сдвига на одну позицию вправо мы попадём на знак = (шаг 13). Это сигнал о том, что входное слово полностью скопировано, поэтому работу МТ надо завершать. С учётом всего сказанного получаем следующую программу для МТ: a b = A B Λ q1,r,r, =,L,q2 поставить = справа от слова q2,l,l,r,q3 налево под 1-й символ q3 A,R,q4 B,R,q5,! анализ и замена очередного символа q4,r,r,r, a,q6 запись a справа q5,r,r,r, b,q6 запись b справа q6,l,l,l, a,r,q3 b,r,q3 возврат, восстановление, к след. символу Отметим, что в этой программе можно избавиться от состояния q6, если объединить его с состоянием q2, предусмотрев в q2 возврат влево как до пустой клетки, так и до символов A и B: a b = A B Λ... q2,l,l,l, a,r,q3 b,r,q3,r,q3 налево до Λ, A или B Задачи для самостоятельного решения Замечания: 1) В задачах рассматриваются только целые неотрицательные числа, если не сказано иное. 2) Под «единичной» системой счисления понимается запись неотрицательного целого числа с помощью палочек должно быть выписано столько палочек, какова величина числа; например: 2, 5, 0 <пустое слово>. 1.1 A={a,b,c}. Приписать слева к слову P символ b (P bp). 1.2 A={a,b,c}. Приписать справа к слову P символы bc (P Pbc). 1.3 A={a,b,c}. Заменить на a каждый второй символ в слове P. 15

16 1.4 A={a,b,c}. Оставить в слове P только первый символ (пустое слово не менять). 1.5 A={a,b,c}. Оставить в слове P только последний символ (пустое слово не менять). 1.6 A={a,b,c}. Определить, является ли P словом ab. Ответ (выходное слово): слово ab, если является, или пустое слово иначе. 1.7 A={a,b,c}. Определить, входит ли в слово P символ a. Ответ: слово из одного символа a (да, входит) или пустое слово (нет). 1.8 A={a,b,c}. Если в слово P не входит символ a, то заменить в P все символы b на с, иначе в качестве ответа выдать слово из одного символа a. 1.9 A={a,b,0,1}. Определить, является ли слово P идентификатором (непустым словом, начинающимся с буквы). Ответ: слово a (да) или пустое слово (нет) A={a,b,0,1}. Определить, является ли слово P записью числа в двоичной системе счисления (непустым словом, состоящем только из цифр 0 и 1). Ответ: слово 1 (да) или слово A={0,1}. Считая непустое слово P записью двоичного числа, удалить из него незначащие нули, если такие есть A={0,1}. Для непустого слова P определить, является ли оно записью степени двойки (1, 2, 4, 8,) в двоичной системе счисления. Ответ: слово 1 (является) или слово A={0,1,2,3}. Считая непустое слово P записью числа в четверичной системе счисления, определить, является оно чётным числом или нет. Ответ: 1 (да) или A={0,1}. Считая непустое слово P записью числа в двоичной системе, получить двоичное число, равное учетверенному числу P (например:) A={0,1}. Считая непустое слово P записью числа в двоичной системе, получить двоичное число, равное неполному частному от деления числа P на 2 (например:) A={a,b,c}. Если P слово чётной длины (0, 2, 4,), то выдать ответ a, иначе пустое слово A={0,1,2}. Считая непустое слово P записью числа в троичной системе счисления, определить, является оно чётным числом или нет. Ответ: 1 (да) или 0. (Замечание: в чётном троичном числе должно быть чётное количество цифр 1.) 1.18 A={a,b,c}. Пусть P имеет нечётную длину. Оставить в P только средний символ A={a,b,c}. Если слово P имеет чётную длину, то оставить в нём только левую половину A={a,b,c}. Приписать слева к непустому слову P его первый символ. 16

17 1.21 A={a,b}. Для непустого слова P определить, входит ли в него ещё раз его первый символ. Ответ: a (да) или пустое слово A={a,b}. В непустом слове P поменять местами его первый и последний символы A={a,b}. Определить, является P палиндромом (перевёртышем, симметричным словом) или нет. Ответ: a (да) или пустое слово A={a,b}. Заменить в P каждое вхождение a на bb A={a,b,c}. Заменить в P каждое вхождение ab на c A={a,b}. Удвоить слово P (например: abb abbabb) A={a,b}. Удвоить каждый символ слова P (например: bab bbaabb) A={a,b}. Перевернуть слово P (например: abb bba) A={0,1}. Считая непустое слово P записью двоичного числа, получить это же число, но в четверичной системе. (Замечание: учесть, что в двоичном числе может быть нечётное количество цифр.) 1.30 A={0,1,2,3}. Считая непустое слово P записью числа в четверичной системе счисления, получить запись этого числа в двоичной системе A={0,1,2}. Считая непустое слово P записью положительного числа в троичной системе счисления, уменьшить это число на A={ }. Считая слово P записью числа в единичной системе счисления, получить запись этого числа в троичной системе. (Рекомендация: следует в цикле удалять из «единичного» числа по палочке и каждый раз прибавлять 1 к троичному числу, которое вначале положить равным 0.) 1.33 A={0,1,2}. Считая непустое слово P записью числа в троичной системе счисления, получить запись этого числа в единичной системе Пусть слово P имеет следующий вид: {... {... n m где один из знаков +, /, или, слева от которого указано n палочек, а справа m палочек. Реализовать соответствующую операцию в единичной системе счисления (в качестве ответа выдать слово, указанное справа от стрелки): а) сложение: {... + {... {... (n 0, m 0) n m n+ m б) вычитание: {... {... {... (n m 0) n m n m в) умножение: {... {... {... (n 0, m 0) n m n m г) деление нацело: {{... /... {... (n 0, m>0, k=n div m) n m k д) взятие остатка: {... {... {... (n 0, m>0, k=n mod m) n m k 17

18 е) максимум: {... {... {... (n 0, m 0, k=max(n,m)) n m k ж) минимум: {... {... {... (n 0, m 0, k=min(n,m)) k n m 1.35 A={ }. Считая слово P записью числа в единичной системе, определить, является ли это число степенью 3 (1, 3, 9, 27,). Ответ: пустое слово, если является, или слово из одной палочки иначе A={ }. Считая слово P записью числа n в единичной системе, получить в этой же системе число 2 n A={ }. Пусть слово P является записью числа 2 n (n=0, 1, 2,) в единичной системе. Получить в этой же системе число n Пусть P имеет вид Q+R, где Q и R непустые слова из символов 0, 1 и 2. Трактуя Q и R как записи чисел в троичной системе счисления (возможно, с незначащими нулями), выдать в качестве ответа запись суммы этих чисел в той же троичной системе Пусть P имеет вид Q R, где Q и R непустые слова из символов 0, 1 и 2. Трактуя Q и R как записи чисел в троичной системе счисления (возможно, с незначащими нулями) и считая, что Q R, выдать в качестве ответа запись разности этих чисел в той же троичной системе Пусть P имеет вид Q=R, где Q и R любые слова из символов a и b. Выдать ответ a, если слова Q и R одинаковы, и пустое слово иначе Пусть P имеет вид Q=R, где Q и R непустые слова из символов 0 и 1. Трактуя Q и R как записи двоичных чисел (возможно, с незначащими нулями), выдать в качестве ответа слово 1, если эти числа равны, и слово 0 иначе Пусть P имеет вид Q>R, где Q и R непустые слова из символов 0 и 1. Трактуя Q и R как записи двоичных чисел (возможно, с незначащими нулями), выдать в качестве ответа слово 1, если число Q больше числа R, и слово 0 иначе A={(,)}. Определить, сбалансировано ли слово P по круглым скобкам. Ответ: Д (да) или Н (нет) A={a,b}. Если в P символов a больше, чем символов b, то выдать ответ a, если символов a меньше символов b, то выдать ответ b, а иначе в качестве ответа выдать пустое слово. 2. Нормальные алгоритмы Маркова В разделе рассматриваются задачи на составление нормальных алгоритмов Маркова. Приводится краткое описание этих алгоритмов, на примерах объясняются основные приёмы их составления и предлагаются задачи для самостоятельного решения. 18

19 2.1 Краткое описание нормальных алгоритмов Маркова Подстановки Интересной особенностью нормальных алгоритмов Маркова (НАМ) является то, что в них используется лишь одно элементарное действие так называемая подстановка, которая определяется следующим образом. Формулой подстановки называется запись вида α β (читается «α заменить на β»), где α и β любые слова (возможно, и пустые). При этом α называется левой частью формулы, а β правой частью. Сама подстановка (как действие) задается формулой подстановки и применяется к некоторому слову Р. Суть операции сводится к тому, что в слове Р отыскивается часть, совпадающая с левой частью этой формулы (т.е. с α), и она заменяется на правую часть формулы (т.е. на β). При этом остальные части слова Р (слева и справа от α) не меняются. Получившееся слово R называют результатом подстановки. Условно это можно изобразить так: P x α y R x β y Необходимые уточнения: 1. Если левая часть формулы подстановки входит в слово Р, то говорят, что эта формула применима к Р. Но если α не входит в Р, то формула считается неприменимой к Р, и подстановка не выполняется. 2. Если левая часть α входит в Р несколько раз, то на правую часть β, по определению, заменяется только первое вхождение α в Р: P x α y α z R x β y α z 3. Если правая часть формулы подстановки пустое слово, то подстановка α сводится к вычеркиванию части α из Р (отметим попутно, что в формулах подстановки не принято как-либо обозначать пустое слово): P x α y R x y 4. Если в левой части формулы подстановки указано пустое слово, то подстановка β сводится, по определению, к приписыванию β слева к слову P: P x R β x Из этого правила вытекает очень важный факт: формула с пустой левой частью применима к любому слову. Отметим также, что формула с пустыми левой и правой частями не меняет слово. Определение НАМ Нормальным алгоритмом Маркова (НАМ) называется непустой конечный упорядоченный набор формул подстановки: 19

20 α1 β1 α 2 β 2... (k 1) α k β k В этих формулах могут использоваться два вида стрелок: обычная стрелка () и стрелка «с хвостиком» (a). Формула с обычной стрелкой называется обычной формулой, а формула со стрелкой «с хвостиком» заключительной формулой. Разница между ними объясняется чуть ниже. Записать алгоритм в виде НАМ значит предъявить такой набор формул. Правила выполнения НАМ Прежде всего, задается некоторое входное слово Р. Где именно оно записано не важно, в НАМ этот вопрос не оговаривается. Работа НАМ сводится к выполнению последовательности шагов. На каждом шаге входящие в НАМ формулы подстановки просматриваются сверху вниз и выбирается первая из формул, применимых к входному слову Р, т.е. самая верхняя из тех, левая часть которых входит в Р. Далее выполняется подстановка согласно найденной формуле. Получается новое слово Р. На следующем шаге это слово Р берется за исходное и к нему применяется та же самая процедура, т.е. формулы снова просматриваются сверху вниз начиная с самой верхней и ищется первая формула, применимая к слову Р, после чего выполняется соответствующая подстановка и получается новое слово Р. И так далее: Р Р Р Следует обратить особое внимание на тот факт, что на каждом шаге формулы в НАМ всегда просматриваются начиная с самой первой. Необходимые уточнения: 1. Если на очередном шаге была применена обычная формула (α β), то работа НАМ продолжается. 2. Если же на очередном шаге была применена заключительная формула (α a β), то после её применения работа НАМ прекращается. То слово, которое получилось в этот момент, и есть выходное слово, т.е. результат применения НАМ к входному слову. Как видно, разница между обычной и заключительной формулами подстановки проявляется лишь в том, что после применения обычной формулы работа НАМ продолжается, а после заключительной формулы прекращается. 3. Если на очередном шаге к текущему слову неприменима ни одна формула, то и в этом случае работа НАМ прекращается, а выходным словом считается текущее слово. Таким образом, НАМ останавливается по двум причинам: либо была применена заключительная формула, либо ни одна из формул не подошла. То и другое считается «хорошим» окончанием работы НАМ. В обоих случаях говорят, что НАМ применúм к входному слову. 20

Московский государственный университет имени М.В. Ломоносова Факультет вычислительной математики и кибернетики В.Н. Пильщиков, В.Г. Абрамов, А.А. Вылиток, И.В. Горячая Машина Тьюринга и алгоритмы Маркова.
МАШИНА ТЬЮРИНГА В ИЗУЧЕНИИ ТЕОРИИ АЛГОРИТМОВ Лебедева Н.Ю. Шуйский филиал Ивановского государственного университета TURING MACHINE IN THE STUDY OF THE THEORY OF ALGORITHMS Lebedeva N. Yu. Shuya branch
СЛОЖЕНИЕ Прибавить 1 к числу означает получить число, следующее за данным: 4+1=5, 1+1=14 и т.д. Сложить числа 5 и значит прибавить к 5 три раза единицу: 5+1+1+1=5+=8. ВЫЧИТАНИЕ Вычесть 1 из числа означает
Задачи и решения отборочного тура олимпиады ДМиТИ 2014-2015 Все задачи, манипуляторы и решения доступны участникам на сайте олимпиады. Все предложенные задачи оценивались одинаковым числом баллов. Графы.
Машина Тьюринга 1 Машина Тьюринга математическое понятие, а не реальная вычислительная машина. MT является математической моделью вычислительного устройства. MT была предложена Аланом Тьюрингом в 1936
Решение задач по машине тьюринга онлайн >>> Решение задач по машине тьюринга онлайн Решение задач по машине тьюринга онлайн Содержимое клетки может меняться в неё можно записать другой символ или стереть
Системы счисления В наше время человек всё время сталкивается с числами. Все мы с детства знакомы с общепринятой записью чисел при помощи арабских цифр. Однако этот способ записи использовался далеко не
Реализуемый алгоритм Мы используем следующую вариацию алгоритма Евклида для вычисления НОД чисел M и N:. a M, b N; 2. t a-b, если t = 0, останов; 3. a t, b min{a,b}, переход на шаг 2. После останова НОД(M,N)
Задачи отборочного тура Олимпиады по дискретной математике и теоретической информатике с решениями (при решении конструктивных задач участник работает с эмуляторами, в решениях приведены картинки их интерфейсов)
Глава B. Компьютерная арифметика Урок B3. Двоичная арифметика Посмотрим, как вы справились с упражнениями из Урока B2. Вот их решения. Упражнения B2-2 a) Таблица размещения гирь выглядит так: в нумерации
Занятие 23 В условиях задач M, x означают соответственно описание машины Тьюринга и входного слова в том формате, который был введён на лекции (и написан в черновике учебника). Задача 23.1. Докажите, что
Раздел 6. Теория алгоритмов. Неформальное понятие алгоритма, его основные черты и свойства. Алфавит, слова, алгоритм в алфавите. Вполне эквивалентные алгоритмы. Определение нормального алгоритма (алгоритма
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Известно множество способов представления чисел. В любом случае число изображается символом или группой символов (словом) некоторого алфавита. Будем называть такие символы
Задания для 11 класса Отборочный этап. Первый тур 1. Кодирование информации. Системы счисления (2 балла) [Перестановки] Сколько существует трехразрядных шестнадцатеричных чисел, для которых будут одновременно
Решение задач на тему «Представление чисел в компьютере» Типы задач: 1. Целые числа. Представление чисел в формате с фиксированной запятой. 2. Дробные числа. Представление чисел в формате с плавающей запятой.
1. Рыцари и лжецы. Логическая схема - 1. Задачи и решения очного тура Олимпиады ДмиТИ-2017-2018 За круглым столом сидят четыре человека. Каждый из них либо рыцарь, либо лжец. Рыцари всегда говорят только
Системы счисления Система счисления способ записи чисел с помощью заданного набора специальных символов (цифр). В вычислительной технике применяются позиционные системы счисления, в которых значение цифры
ЛЕКЦИЯ 3. Алгоритмы обработки одномерных массивов. Цель лекции: Знакомство с понятием массива. Приобретение навыков построения алгоритмов предназначенных для обработки одномерных массивов. 6. Алгоритмы
Демонстрационный вариант ЕГЭ 2019 г. задание 6 На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом. 1) Строится двоичная запись числа N. 2) К этой записи
Введение в системы счисления А.А. Вылиток Система счисления это способ записи чисел с помощью заданного набора специальных знаков (цифр). Существуют позиционные и непозиционные системы счисления. В непозиционных
Часть III Языки, грамматики, автоматы 137 Глава 10 Языки и конечные автоматы 10.1 Язык Дика Как мы знаем, правильные скобочные структуры перечисляются числами Каталана. Выпишем все правильные скобочные
Муниципальный этап всероссийской олимпиады школьников по информатике Москва, декабря 0 г. Задания для 7 8 классов Каждая задача оценивается в 0 баллов. Итоговый балл выставляется как сумма баллов за задачи
Виртуальные машины Введение Свыше сорока лот назад выдающийся американский математик Эмиль Л. Пост опубликовал в «Журнале символической логики» статью «Финитные комбинаторные процессы, формулировка!» (ее
Югорский физико-математический лицей ВП Чуваков Задача С6 (Теория чисел на ЕГЭ) Учебно-методическое пособие Ханты-Мансийск 0 ВП Чуваков Задача С6 (Теория чисел на ЕГЭ): Учебнометодическое пособие, - Ханты-Мансийск,
9 КЛАСС 1. В одной из клеток бесконечной клетчатой бумаги находится робот, которому могут быть отданы следующие команды: вверх (робот перемещается на соседнюю клетку сверху); вниз (робот перемещается на
Системы счисления Система счисления это способ записи чисел с помощью заданного набора специальных знаков (цифр). Существуют позиционные и непозиционные системы счисления. В непозиционных системах вес
Системы счисления Система счисления способ описания чисел с помощью знаков определенного алфавита по известным правилам. Позиционные системы счисления В позиционной системе счисления значение цифры зависит
К. Поляков, 009-06 6- (базовый уровень, время 4 мин) Тема: Поиск алгоритма минимальной длины для исполнителя. Что нужно знать: исполнитель это человек, группа людей, животное, машина или другой объект,
Лекция 5 Основы представления информации в цифровых автоматах Позиционные системы счисления Системой счисления называется совокупность приемов и правил для записи чисел цифровыми знаками. Любая предназначенная
Элементы теории сложности Машина Тьюринга Алан Тьюринг (23.06.1912-7.06.1954) (Alan Mathison Turing) Английский математик, логик, криптограф. В 1936 году предложил абстрактную вычислительную «Машина Тьюринга»,
Министерство образования и науки Российской Федерации Государственное образовательное учреждение профессионального образования Российской Федерации «Ростовский государственный университет» М. Э. Абрамян
10 КЛАСС 1. Действительные числа удовлетворяют соотношениям: Найдите все возможные тройки чисел, где Решение. Заметим, что Обозначим и Вычитая друг из друга эти равенства, получим Предположим, что все
Приложение к статье Горбунов К.Ю., Любецкий В.А. «Линейный алгоритм минимальной перестройки структур» Доказательство леммы 3. Жестким назовём блок, ограниченный с обеих сторон общими генами, полужёстким
Приложение 1 Практикум к главе 2 «Представление информации в компьютере» Практическая работа к п. 2.1 Пример 2.1. Представьте в виде разложения по степеням основания числа 2466,675 10, 1011,11 2. Для десятичного
Заочный физико-математический лицей «Авангард» Е. Н. Филатов АЛГЕБРА 8 Экспериментальный учебник Часть 1 МОСКВА 2016 СОДЕРЖАНИЕ 1. Делимость. 2. Чёт нечет 3. Множества. 4. Забавные задачи. 5. Комбинаторика
Задачник по информатике ученика (цы) 11 физико-математического класса средней школы 36 г.владимира Часть II 2016-2017 г. 2 1. Алгоритмизация. 1.1 Предлагается некоторая операция над двумя произвольными
Тема 7. Представление информации в ЭВМ.. Единицы информации. Бит - (bit-biry digit - двоичный разряд) наименьшая единица информации - количество её, необходимое для различения двух равновероятных событий.
И. В. Яковлев Материалы по математике MathUs.ru Содержание Десятичная запись 1 Всероссийская олимпиада школьников по математике................ 1 2 Московская математическая олимпиада........................
Тема 1: Системы линейных уравнений А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для физиков-инженеров
Глава 5 Элементы теории алгоритмов 31 Уточнение понятия алгоритма Ключевые слова: алгоритм теория алгоритмов универсальный исполнитель машина Тьюринга машина Поста нормальный алгорифм Маркова Зачем нужно
Решение задач на тему «Представление чисел в компьютере». Типы задач. 1. Целые числа. Представление чисел в формате с фиксированной запятой. 2. Дробные числа. Представление чисел в формате с плавающей
А. Шень Игры и стратегии с точки зрения математики, МЦНМО Простые игры и классификация позиций На столе лежит 12 спичек. Играющие по очереди могут взять от одной до трёх спичек. Кто не может сделать ход
Теория алгоритмов 79 3.2. Нормальные алгоритмы j Пусть A алфавит, не содержащий символов. и. Обыкновенной формулой подстановок называется запись вида P Q, где P и Q некоторые слова в алфавите A. Заключительной
ЛЕКЦИЯ 2. Алгоритмы циклической структуры. Цель лекции: Знакомство с понятием алгоритма циклической струк туры. Приобретение навыков построения алгоритмов циклической с трук т уры. 5. Алгоритмы циклической
Лекции по Математике. Вып. ТММ-1 Ю. В. Чебраков ТЕОРИЯ МАГИЧЕСКИХ МАТРИЦ Санкт-Петербург, 2010 УДК 511+512 ББК 22 Ч345 Р е ц е н з е н т ы: Доктор физико-математических наук, профессор С.-Петерб. техн.
Практическая работа. Формы представления числовой информации на компьютере. Часть I. Системы счисления. Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита
Московский физико-технический институт Факультет инноваций и высоких технологий Математическая логика и теория алгоритмов, осень 2018 Семинар 1: язык записи формальных утверждений, с решениями некоторых
Лекция 16. Универсальная машина Тьюринга Дискретная математика, ВШЭ, факультет компьютерных наук (Осень 2014 весна 2015) Важнейшим свойством вычислимых функций является существование универсальной вычислимой
16 (повышенный уровень, время мин) Тема: Кодирование чисел. Системы счисления. Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем, 15, из системы
2015 Регулярные выражения Решения задач отборочного тура (два варианта) Вариант 1 Постройте регулярное выражение, описывающее множество слов из букв a и b, из которого удалены все слова, задаваемые регулярным
Который, позаимствовав идею у Эмиля Поста, придумал её, как считается, в 1936 году. Несмотря на довольно сложное формальное определение, идея в принципе проста. Чтобы понять её, давайте прогуляемся по страницам Википедии.
Первым делом мы попадаем на страничку, которая, собственно, так и называется: «машина Тьюринга ».
Машина Тьюринга
Машина Тьюринга (МТ) - математическая абстракция, представляющая вычислительную машину общего вида. Была предложена Аланом Тьюрингом в году для формализации понятия алгоритма .
Машина Тьюринга является расширением модели конечного автомата и, согласно тезису Чёрча - Тьюринга , способна имитировать (при наличии соответствующей программы) любую машину, действие которой заключается в переходе от одного дискретного состояния к другому.
В состав Машины Тьюринга входит бесконечная в обе стороны лента , разделённая на ячейки, и управляющее устройство с конечным числом состояний.
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
В управляющем устройстве содержится таблица переходов , которая представляет алгоритм, реализуемый данной Машиной Тьюринга. Каждое правило из таблицы предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния Машины Тьюринга могут быть помечены как терминальные , и переход в любое из них означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной , если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила, и недетерминированной в противном случае.
Итак, машина Тьюринга - математическая абстракция , умозрительное построение человеческого разума: в природе её нет. Или есть? Сразу приходит на ум, как работает живая клетка . Хотя бы два примера.
1. Для производства белков в клетке с помощью сложно устроенного фермента - РНК-полимеразы - считывается информация с ДНК, своего рода информационной ленты машины Тьюринга. Здесь, правда, не происходит перезапись ячеек самой ленты, но в остальном процесс весьма похож: РНК-полимераза садится на ДНК и двигается по ней в одном направлении, при этом она синтезирует нить РНК - нуклеиновой кислоты, сходной с ДНК. Готовая РНК, отсоединяясь от фермента, несёт информацию к клеточным органеллам, в которых производятся белки.
2. Ещё более похож на машину Тьюринга процесс исправления ошибок в ДНК - её репарация. Здесь ДНК-полимераза вместе с другими белками двигается по ленте ДНК и считывает обе её половинки (геномная ДНК, как известно, представляет собой две переплетенных нити, несущих одну и ту же информацию). Если информация в половинках не совпадает, ДНК-полимераза принимает одну из них за образец и «правит» другую.
Такая аналогия не нова, и в Википедии она тоже описана в статье «Молекулярный компьютер »:
Молекулярный компьютер
Биомолекулярные вычисления или молекулярные компьютеры или даже ДНК - или РНК -вычисления - все эти термины появились на стыке таких различных наук как молекулярная генетика и вычислительная техника.
Биомолекулярные вычисления - это собирательное название для различных техник, так или иначе связанных с ДНК или РНК. При ДНК-вычислениях данные представляются не в форме нулей и единиц, а в виде молекулярной структуры, построенной на основе спирали ДНК. Роль программного обеспечения для чтения, копирования и управления данными выполняют особые ферменты .
Основой всей системы хранения биологической информации, а стало быть, и ДНК-компьютеров, является способность атомов водорода , входящих в азотистые соединения (аденин , тимин , цитозин и гуанин), при определенных условиях притягиваться друг к другу, образуя невалентно связанные пары. С другой стороны, эти вещества могут валентно связываться с сочетаниями молекулы сахара (дезоксирибозы) и фосфата , образуя так называемые нуклеотиды . Нуклеотиды, в свою очередь, легко образуют полимеры длиной в десятки миллионов оснований. В этих супермолекулах фосфат и дезоксирибоза играют роль поддерживающей структуры (они чередуются в цепочке), а азотистые соединения кодируют информацию.
Молекула получается направленной: начинается с фосфатной группы и заканчивается дезоксирибозой. Длинные цепочки ДНК называют нитями, короткие - олигонуклеотидами. Каждой молекуле ДНК соответствует еще одна ДНК - так называемое дополнение Ватсона - Крика . Она имеет противоположную направленность, нежели оригинальная молекула. В результате притяжения аденина к тимину и цитозина к гуанину получается знаменитая двойная спираль, обеспечивающая возможность удвоения ДНК при размножении клетки. Задача удвоения решается с помощью специального белка-энзимы - полимеразы. Синтез начинается только если с ДНК прикреплен кусочек ее дополнения, Данное свойство активно используется в молекулярной биологии и молекулярных вычислениях. По сути своей ДНК + полимераза - это реализация машины Тьюринга , состоящая из двух лент и программируемого пульта управления. Пульт считывает данные с одной ленты, обрабатывает их по некоторому алгоритму и записывает на другую ленту. Полимераза также последовательно считывает исходные данные с одной ленты (ДНК) и на их основе формирует ленту как бы с результатами вычислений (дополнение Ватсона - Крика).
Немножко фантастические перспективы только подогревают наше любопытство. Между тем, мы еще не всё выяснили относительно машины Тьюринга. Как вы помните, в статье из Википедии её назвали расширением конечного автомата. Что же это такое конечный автомат? На него, к счастью, даётся ссылка. Заходя по ней, узнаём, что:
Конечный автомат
Абстрактные автоматы образуют фундаментальный класс дискретных моделей как самостоятельная модель, и как основная компонента машин Тьюринга , автоматов с магазинной памятью , конечных автоматов и других преобразователей информации.
С каждым определением мы всё больше вторгаемся в область чистой математики. Язык становится строже, появляются формальные определения, состоящие из математических символов. Если двигаться дальше, мы придём к теории алгоритмов и теории вычислимости. Путешествовать по страницам Википедии можно долго, но лучше запастись водой и едой, на случай забредания в пустыни аксиом и определений, или хотя бы надёжными ссылками на учебники по математике, например http://www.mccme.ru/free-books/ , или статьи журнала «Потенциал» ;)
Надеюсь, после этого объяснения вам стало немного яснее, что же такое машина Тьюринга?
Давайте вернёмся к истории этого термина.
Итак, как мы уже упоминали, Алан Тьюринг поведал миру о своей машине в 1937 году в так называемом Тезисе Чёрча-Тьюринга. Про Алана Тьюринга - первого хакера и пионера информатики, как написано на мемориальной доске гостиницы, где он родился, поведает нам статья «Алан Тьюринг». Текст статьи полностью приводить здесь не будем, но она и сама по себе не очень подробная.
Алан Тьюринг
Тьюринг, Алан Матисон (23 июня 1912 - 7 июня 1954) - английский математик, логик, криптограф, изобретатель Машины Тьюринга.
В самой статье больше про труды Тьюринга: помимо текста про машину Тьюринга, который мы еще приведем дальше, повествуется о том, что он работал над «проблемой зависания» (Забавно, не так ли? Компьютеров еще не было, и системы Windows тоже, а проблема зависания уже была.); героическая история про то, как Тьюринг взломал код «Энигмы» во время Второй Мировой Войны и тем самым спас Великобританию; факт о том, что он является основателем теории искусственного интеллекта, а также упоминание о знаменитом тесте Тьюринга. Сейчас этот тест уже не так часто используется как завязка научно-фантастического рассказа, однако проблема человеческого в машине всегда останется классикой, как и романы Айзека Азимова и Станислава Лема.
Несмотря на свою старомодность, тест Тьюринга всплыл неожиданным образом в современном мире общения по интернету. К примеру, можно встретить текст диалога двух пользователей ICQ, один из которых является «ботом», и задача - определить, какой именно. Или к Вам может постучаться незнакомый пользователь, возможно, ICQ-робот. Узнаете ли вы его? Изучая теорию, Вы, возможно, сумеете вовремя применить тест Тьюринга и не останетесь обмануты. Начать изучение можно с соответствующей статьи в Википедии, а затем пройтись по ссылкам, приводимым в конце статьи:
Тест Тьюринга
Тест Тьюринга - тест, предложенный Аланом Тьюрингом в 1950 г. в статье «Вычислительные машины и разум» (Computing machinery and intelligence) для проверки, является ли компьютер разумным в человеческом смысле слова.
Судья (человек) переписывается на естественном языке с двумя собеседниками, один из которых - человек, другой - компьютер. Если судья не может надёжно определить, кто есть кто, компьютер прошёл тест. Предполагается, что каждый из собеседников стремится, чтобы человеком признали его. С целью сделать тест простым и универсальным, переписка сводится к обмену текстовыми сообщениями.
Переписка должна производиться через контролируемые промежутки времени, чтобы судья не мог делать заключения исходя из скорости ответов. (Во времена Тьюринга компьютеры реагировали медленнее человека. Сейчас это правило необходимо, потому что они реагируют гораздо быстрее, чем человек).
Тест был инспирирован салонной игрой, в ходе которой гости пытались угадать пол человека, находящегося в другой комнате, путём написания вопросов и чтения ответов. В оригинальной формулировке Тьюринга, человек должен был притворяться человеком противоположного пола, а тест длился 5 минут. Сейчас эти правила не считаются необходимыми и не входят в спецификацию теста.
Тьюринг предложил тест, чтобы заменить бессмысленный, по его мнению, вопрос «может ли машина мыслить?» на более определённый.
Тьюринг предсказал, что компьютеры в конечном счёте пройдут его тест. Он считал, что к 2000 году, компьютер с памятью 1 миллиард бит (около 119 Мб) в ходе 5-минутного теста сможет обмануть судей в 30 % случаев. Это предсказание не сбылось. (Правда, на первом конкурсе Лебнера компьютерная программа «PC Therapist» на IBM PC 386 смогла ввести в заблуждение 5 судей из 10, но ей не засчитали результат, а в 1994 году конкурс усложнили.) Тьюринг также предсказал, что сочетание «мыслящая машина» не будет считаться оксюмороном , а обучение компьютеров будет играть важную роль в создании мощных компьютеров (с чем большинство современных исследователей согласны).
Пока что ни одна программа и близко не подошла к прохождению теста. Такие программы, как Элиза (ELIZA), иногда заставляли людей верить, что они говорят с человеком, как, например, в неформальном эксперименте, названном AOLiza. Но такие «успехи» не являются прохождением теста Тьюринга. Во-первых, человек в таких беседах не имел никаких оснований считать, что он говорит с программой, в то время как в настоящем тесте Тьюринга человек активно пытается определить, с кем он беседует. Во-вторых, документированые случаи обычно относятся к таким чатам, как IRC , где многие беседы отрывочны и бессмысленны. В-третьих, многие пользователи IRC используют английский как второй или третий язык, и бессмысленный ответ программы, вероятно, спишется ими на языковый барьер. В-четвертых, многие пользователи ничего не знают об Элизе и ей подобных программах и не могут распознать совершенно нечеловеческие ошибки, которые эти программы допускают.
Ежегодно производится соревнование между разговаривающими программами, и наиболее человекоподобной, по мнению судей, присуждается приз Лебнера (Loebner). Есть дополнительный приз для программы, которая, по мнению судей, пройдёт тест Тьюринга. Этот приз ещё не присуждался.
Самый лучший результат в тесте Тьюринга показала программа A.L.I.C.E. выиграв тест 3 раза (в 2000, 2001 и 2004).
Ссылки
- Тьюринг А. М. Вычислительные машины и разум. // В сб.: Хофштадер Д., Деннет Д. Глаз разума. - Самара: Бахрах-М, 2003. - С. 47-59.
- Книга на английском: Roger Penrose «The Emperor’s New Mind».
- Статья Алана Тьюринга:
- Alan Turing, «Computing Machinery and Intelligence», Mind, vol. LIX, no. 236, October 1950, pp. 433-460.
- В сети:
- Статья Дж. Оппи (G. Oppy) и Д. Дави (D. Dowe) о тесте Тьюринга из Стэнфордской Философской Энциклопедии (на английском)
- «Turing Test: 50 Years Later» обзор 50-летней работы над тестом Тьюринга, с точки зрения 2000 г. (на английском).
Возвращаемся опять к машине Тьюринга. В выдержке из статьи про Алана Тьюринга утверждается, что впервые понятие машины Тьюринга было предложено в составе т. н. тезиса Чёрча-Тьюринга:
Выдержка из статьи Википедии «Алан Тьюринг»
Любая интуитивно вычислимая функция является частично вычислимой, или, эквивалентно, может быть вычислена с помощью некоторой машины Тьюринга.
Алан Тьюринг высказал предположение (известное как Тезис Чёрча-Тьюринга), что любой алгоритм в интуитивном смысле этого слова может быть представлен эквивалентной машиной Тьюринга. Уточнение представления о вычислимости на основе понятия машины Тьюринга (и других эквивалентных ей понятий) открыло возможности для строгого доказательства алгоритмической неразрешимости различных массовых проблем (то есть проблем о нахождении единого метода решения некоторого класса задач, условия которых могут варьироваться в известных пределах). Простейшим примером алгоритмически неразрешимой массовой проблемы является так называемая проблема применимости алгоритма (называемая также проблемой остановки). Она состоит в следующем: требуется найти общий метод, который позволял бы для произвольной машины Тьюринга (заданной посредством своей программы) и произвольного начального состояния ленты этой машины определить, завершится ли работа машины за конечное число шагов, или же будет продолжаться неограниченно долго.
В статье под названием «Те́зис Чёрча-Тью́ринга» про него пишут так:
Те́зис Чёрча-Тью́ринга
Те́зис Чёрча-Тью́ринга - фундаментальное утверждение для многих областей науки, таких, как теория вычислимости , информатика , теоретическая кибернетика и др. Это утверждение было высказано Алонзо Чёрчем и Аланом Тьюрингом в середине 1930-х годов.
В самой общей форме оно гласит, что любая интуитивно вычислимая функция является частично вычислимой , или, эквивалентно, может быть вычислена с помощью некоторой машины Тьюринга .
Тезис Чёрча-Тьюринга невозможно строго доказать или опровергнуть, поскольку он устанавливает «равенство» между строго формализованным понятием частично вычислимой функции и неформальным понятием «интуитивно вычислимой функции».
Физический тезис Чёрча-Тьюринга гласит: Любая функция, которая может быть вычислена физическим устройством, может быть вычислена машиной Тьюринга .
С этого перекрёстка можно двинуться в сторону, к примеру, теории вычислимости. А можно попытаться выяснить, кто такой этот загадочный Чёрч, вместе с которым Алан Тьюринг выдвинул свой тезис.
Универсальная машина Тьюринга
Универсальной машиной Тью́ринга называют машину Тьюринга , которая может заменить собой любую машину Тьюринга. Получив на вход программу и входные данные, она вычисляет ответ, который вычислила бы по входным данным машина Тьюринга, чья программа была дана на вход.
Формальное определение
Программу любой детерминированной машины Тьюринга можно записать, используя некоторый конечный алфавит, состоящий из символов состояния, скобок, стрелки и т. п.; обозначим этот машинный алфавит как Σ 1 {\displaystyle \Sigma _{1}} . Тогда универсальной машиной Тьюринга U для класса машин с алфавитом Σ 2 {\displaystyle \Sigma _{2}} и k входными лентами называется машина Тьюринга с k+1 входной лентой и алфавитом Σ 1 ∪ Σ 2 {\displaystyle \Sigma _{1}\cup \Sigma _{2}} такая, что если подать на первые k лент входное значение, а на k+1 - правильно записанный код некоторой машины Тьюринга , то U выдаст тот же ответ, какой выдала бы на этих входных данных M 1 {\displaystyle M_{1}} , или будет работать бесконечно долго, если M 1 {\displaystyle M_{1}} на этих данных не остановится.
Теорема об универсальной машине Тьюринга утверждает, что такая машина существует и моделирует другие машины с не более чем квадратичным замедлением (то есть если исходная машина произвела t шагов, то универсальная произведёт не более ct 2 ). Доказательство у этой теоремы конструктивное (такую машину несложно построить, надо только аккуратно её описать). Теорема была предложена и доказана Тьюрингом в 1936-37 г.
Программная реализация на языке программирования Delphi достаточно проста. С одной из таких реализаций можно ознакомиться на сайте http://kleron.ucoz.ru/load/24-1-0-52 . Предусмотрена возможность загрузки и сохранения в файл Excel.
Недетерминированная машина Тьюринга
Вероятностная машина Тьюринга
Обобщение детерминированной машины Тьюринга, в которой из любого состояния и значений на ленте машина может совершить один из нескольких (можно считать, без ограничения общности - двух) возможных переходов, а выбор осуществляется вероятностным образом (подбрасыванием монетки).
Вероятностная Машина Тьюринга похожа на недетерминированную машину Тьюринга, только вместо недетерминированного перехода машина выбирает один из вариантов с некоторой вероятностью.
Существует также альтернативное определение:
Вероятностная машина Тьюринга представляет собой детерминированную машину Тьюринга, имеющую дополнительно аппаратный источник случайных битов, любое число которых, например, она может «заказать» и «загрузить» на отдельную ленту и потом использовать в вычислениях обычным для МТ образом.
Класс алгоритмов, завершающихся за полиномиальное время на вероятностной машине Тьюринга и возвращающих ответ с ошибкой менее 1/3, называется классом BPP .